预测强度及其在聚类分析中的应用
2009 年 11 月 08 日 | 分类于 学习中打了一个草稿,先发到这里吧,等修改好了就往COS主站上发一份。:)
聚类分析的广泛应用想必不用多说,但大家在做聚类的时候可能经常会遇到一个比较头疼的问题,那就是聚类数的选择。聚类数的选择其实很有讲究:太少了,可能样本点不能很好地区分开来;太多了,结果又往往不好解释。因此聚类数的选择其实是一个很重要的问题。 但是在实际情形中,聚类数的选择又经常显得比较主观,我们可能会说,“依据这个问题的实际意义,应该聚成××类”,但是这样容易造成一个后果,就是甲说甲有理,乙说乙有理,孰是孰非难以分辨。 或者我们会采用层次聚类法,因为它不需要事先对聚类数进行指定,但面对那一棵繁茂倒长的树,我们手中的剪刀可能依然是无从下手。 而像k-means这样的聚类方法就更不用说了,k是必须要事先指定好的,否则连聚类的过程都完成不了。
于是我们很自然地要提出这样一个问题:有没有这样一种方法,能为我们聚类数的确定提供一些理论上的依据?关于这一点,也许已经有很多人给出过他们的建议,而本文要为大家介绍的是Tibshirani等大牛们于2001年提出的一种基于“预测强度”的确定聚类数的方法。文章的原文请点击这里,注意这是ps格式的,可能需要用GSview之类的工具打开。本文所讲的大概只是文章的小部分内容,有兴趣的读者可以仔细研究一下那篇文章。
一、预测强度的思想
预测强度的表达是一大串数学符号,为了直观地说明它的含义,我们先来思考一个问题:什么样的聚类是一个好的聚类?如果我们回答了这个问题,而且可以把聚类的效果表达成聚类数k的函数,那么聚类数的选取其实就变成一个最优化的过程了。
对于这个问题,不同的人会有不同的回答,但大体的想法应该差不多,就是希望聚类的结果能将样本点尽可能地分开。事实上,聚类的过程就是围绕这个思想而来的。我们一般认为,类与类之间的距离越远,它们分得也就越开,于是我们就定义了点与点的距离,点与类的距离,类与类的距离,然后以此为依据将类分开。
但是我们其实可以换一种思路,那就是用分类的思想去理解聚类。众所周知,分类和聚类一个是有监督一个是无监督,但它们并不是完全没有联系。试想,当一个数据集进行聚类之后,它就自然而然地具有了分类的能力,换句话说,拿一批新的样品过来,原来的数据就可以对新数据进行分类,于是新数据就可以得到一列记录了每个样品分类的编号(假定叫编号1)。另一方面,新的数据自身也可以进行聚类,也可以得到一个分类编号(假定叫编号2),那么编号1和编号2之间是否一致就决定了聚类的结果是否具有可预测性。我们之前说的要将样本点尽可能地分开,其实就是希望聚类结果能对新样本进行准确而良好的预测,这正是预测强度方法最核心的思想,也是“预测强度”名称的由来。
二、预测强度的计算
说到预测的能力,也许大家会很自然地想到分类器的误分率。不错,被正确预测的样品的比例是判断分类器预测能力的一个重要指标,但是如果出现下面的情形:有5个新样本点,自身聚类的编号分别是1,1,1,2,2,而用已有数据判别的结果是2,2,2,1,1,如果直接拿它们进行对比的话,判对率是0,但实际上,这两组编号应该是完全吻合的。其中的原因就在于,聚类的编号其实是无序的,是可以任意调换的,如果我们要测量两组编号的吻合性,就需要消除其中序的概念。
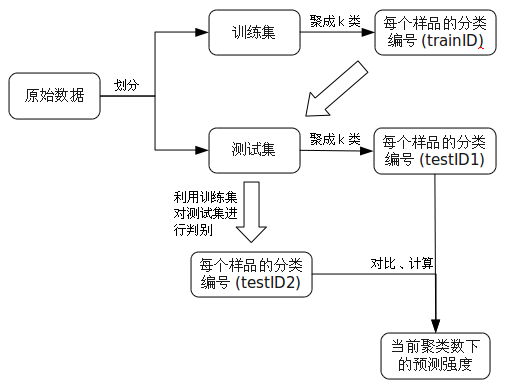
关于这个问题的解决后面会提及,现在还是从预测强度的计算着手。拿到一批数据,首先将其随机划分为训练集和测试集,然后分别对这两组数进行聚类(按需要选定一种聚类方法,并先假设聚类数k是已知的),这样训练集和测试集就分别得到了一列类别编号(记为trainID和testID1)。接下来用训练集及其编号对测试集进行判别,于是测试集就获得了第二列编号(记为testID2)。下面的工作就是衡量testID1和testID2之间的一致性程度。
预测强度的做法是,先考虑testID1里面的每一个类,比如编号为1的所有样品,如果它们一共有n_k1个(k是总的聚类数),那么它们的两两配对就有n_k1(n_k1-1)/2种;接下来就考察每一种配对下,这两个样品是否在testID2中也被分在同一个组;计算出那些在testID2中也被分在同一组的配对所占的比例,然后重复这个过程,对所有的k个类都计算出相应的值;最后对这k个数值取最小值,就是当前聚类数k下的预测强度。
用一张流程图来说明,就是:
再举一个直观的例子。假设有一批新样品,自身聚类的编号是
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
被判别的编号是
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | |
| 1 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | |
那么,对于自身聚类中的第1个类,可以作出下面的这个矩阵:
| X1 | X2 | X3 | X4 | X5 | X6 | |
| X1 | 1 | 0 | 1 | 1 | 0 | |
| X2 | 0 | 1 | 1 | 0 | ||
| X3 | 0 | 0 | 1 | |||
| X4 | 1 | 0 | ||||
| X5 | 0 | |||||
| X6 |
其中如果两个点在判别编号中也一样,就记为1,否则就记为0。于是很容易得出判对的比例是7/15。
同理,另一个类别的矩阵是
| X7 | X8 | X9 | X10 | |
| X7 | 1 | 1 | 0 | |
| X8 | 1 | 0 | ||
| X9 | 0 | |||
| X10 |
比例为3/6=1/2。于是,当前聚类数2下的预测强度就是7/15和1/2中的最小值,即7/15。
三、预测强度的应用
有了上面的思想和计算方法,预测强度的应用就很直接了。就拿确定聚类数来说,我们只要算出各个聚类数下的预测强度,然后找出其中的最大值对应的k就可以了。
举一个原文中的例子,下图是作者做的三个模拟实验,其中左边的三幅图表示实际处理的三组数据,右边是对应的预测强度计算结果。在右边的图中,横轴表示尝试使用的聚类数,纵轴是每一个聚类数下的预测强度,将这些点连成图线,就可以直观地看出预测强度随聚类数的变化情况。
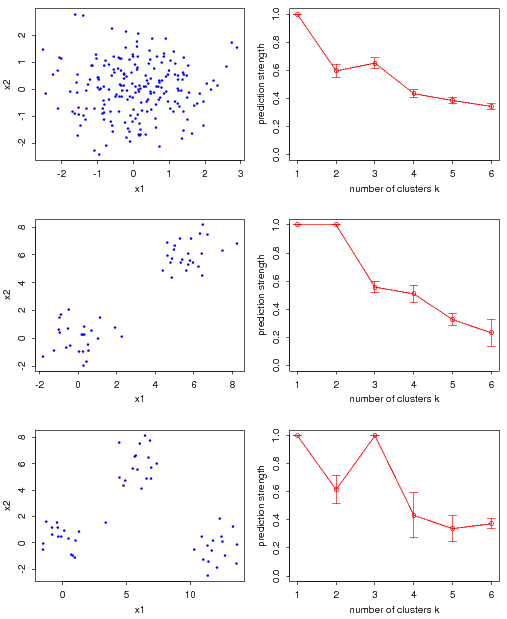 从右边第一幅图可以看出,预测强度在k>1时都比较小,尚不足70%,说明聚类数在大于1时表现都不太良好,这正好与左图反映的情况是一致的——数据本身就十分混杂,应该只有一类;
而右边第二幅和第三幅图分别在k=2和k=3时达到了高峰,这与左图反映的数据形态也是完全吻合的。
从右边第一幅图可以看出,预测强度在k>1时都比较小,尚不足70%,说明聚类数在大于1时表现都不太良好,这正好与左图反映的情况是一致的——数据本身就十分混杂,应该只有一类;
而右边第二幅和第三幅图分别在k=2和k=3时达到了高峰,这与左图反映的数据形态也是完全吻合的。
在上述的例子中,预测强度为我们找到了“最正确”的聚类数,但这毕竟是模拟的结果。在实际应用的过程中,有以下几个问题还需要考虑一番:
1、交叉验证
在计算预测强度的过程中,我们需要对数据进行随机划分,而这种带有随机性的算法我们最担心的就是结果的稳定性。如果我们手头上的数据量比较大的话,其实可以采用交叉验证的方式,比如把数据随机等分成5份,每一次从中取出一份作为测试集,其余的为训练集,然后计算出一个预测强度;重复这个步骤,直到每一份都轮了一遍,这样总共就算出了5个数值;对这5个数取平均,就是用5折交叉验证得出的平均预测强度。
2、k=1时的预测强度
这是一个值得思考的问题,因为事实上,当k=1,即数据只聚成一类时,预测强度是恒为1的。原因很简单,那就是因为,只要是聚成一类,那么所有的样本点都会落在同一个类中,因此没有任何一个配对会被错判。但是此时,我们并不能说聚类数为1时就一定是最好的——如果真是这样的话,聚类还有什么意义呢?
所以这时候,我们就不能单纯地用最优化的思想去看待这个问题。我们应该首先看k>1时预测强度大致的取值,如果取值都比较小,那么我们也许可以认为这个数据本身就比较混杂,不适合做聚类,即承认k=1;而如果在某个聚类数k_0>1上预测强度达到了0.8、0.9这样的水平,那也许我们还是应该认为数据是有聚类的必要的。
从之前的图中我们也可以得到一些启发:第一幅图的预测强度在k>1时就“一蹶不振”了,而后面两幅都在某个大于1的位置上有了一个接近于1的取值(在这个比较理想的模拟条件下其实就是等于1了),因此我们认为第一组数据应该聚成一类,而第二、第三组数据分别聚成两类和三类。
3、聚类和分类方法的选择
在计算预测强度的过程中聚类算法和分类算法都有所涉及,但文章的原文中并没有太多地涉及相应方法的选择。我个人认为,选择什么样的聚类和分类方法主要取决于数据的特点。如果数据量比较大,可能层次聚类法算起来就比较困难,这时可以用k-means等方法;而至于分类,也可以用一些比较快速的基于距离的判别法,比如LDA、QDA等。但总的来说,方法的选取还是相对自由和宽松的。
四、一些思考
在文章的原文中,作者只是用预测强度来选择合适的聚类数,但是回到之前提出的那个问题,当我们把预测强度也作为衡量聚类效果好坏的一个标准的时候,被优化的因素按理就可以变得更多了。比如说,变量的选择也可以被纳入到优化的框架中,因为在分类的时候,并不是变量越多预测的效果就越好。于是,我们可以将聚类数和变量子集进行二维的优化,来得到各自最优的取值。
最后总结一下,预测强度其实就是把分类的思想应用到聚类之中,以预测的能力作为聚类效果好坏的标准,进而以这个标准来选取最佳的聚类数或其它的影响因素。但还是那句话,任何一种统计方法都有其适用的范围,实际使用的过程中,可能并不总能得到很好的结果,这时就还需要对数据本身进行更深入的认识,才能得出可靠的结论。
附:计算预测强度的R代码,供参考。
psk=function(train,test,k)
{
cl.train=kmeans(train,k)$cluster;
cl.test=kmeans(test,k)$cluster;
n=table(cl.test);
library(MASS);
train=cbind(as.data.frame(train),cl=cl.train);
lda.model=lda(cl~.,data=train);
cl.test.pred=predict(lda.model,test)$class;
if(is.vector(test)) test=as.matrix(test,ncol=1);
ps=numeric(k);
for(i in 1:k)
{
index=(1:dim(test)[1])[cl.test==i];
pred=cl.test.pred[index];
ps[i]=(sum(outer(pred,pred,"=="))-n[i])/n[i]/(n[i]-1);
}
return(min(ps));
}


