用过Photoshop或者GIMP的朋友应该都对高斯模糊这个工具比较熟悉。我虽然对作图不怎么了解，但隐约感觉投影效果中的阴影就是用高斯模糊做成的。下面是一个简单的高斯模糊的示例（图片来源），还有一个真相请看这里：

其中右半部分应用了高斯模糊的效果，看起来就像是在画面上盖了一层毛玻璃。那么这种效果是怎么实现的呢？其实啊，看到高斯这个名号，就不由地让人警觉起来——他的渗透力实在太大了。

在网上找了几篇介绍高斯模糊的文章——维基、博客一、博客二，看着里面的几个公式那叫一个亲切啊，虽然世间“高斯”的含义有很多，但此处的高斯自然就是统计中最熟悉不过的正态分布了。维基中对高斯模糊的解释挺吓人，“图像的高斯模糊过程就是图像与正态分布做卷积”，像我这种数学根基不好的看到这里便肃然起敬，只好通过后面博客中的例子来理解了。

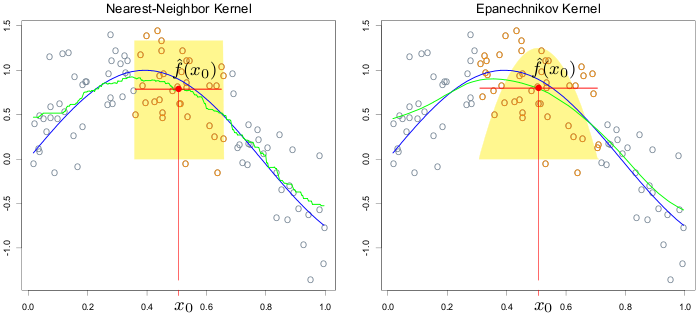
看来看去，终于看到了一些熟悉的东西，原来高斯模糊和平滑技术中的核函数回归是一回事。先看下面这两张图（从The Elements of Statistical Learning中截的）：

其中散点图代表了y与x之间的对应关系。可以看出，随着x的增大，y的取值会上下起伏，变动比较大；而图中的蓝线非常光滑，同时又体现了散点图的大致走向，因此可以认为蓝线是这堆散点的一种规律性描述。事实上，图中的散点就是在蓝线的基础上加以随机误差而生成的。在大多数的情况下，我们能够获得的信息就是图中的散点，而蓝线则是我们想要得到的规律，于是我们面临的问题就是用这些已知的数据去估计未知的结构。图中的绿线做的就是这件事，左图用的是最近邻法，右图是用的是Epanechnikov核函数法。具体的计算细节在此不多加讨论，但总结起来它们都做了同样一件事：为了估计某个点x0处y的取值y0，先在x0处开一扇窗子，让某些点进入窗子，其它的排除在外；这样一来，窗子内的每个点xi都有其对应的y的取值yi，然后用某种权重将这些yi组合起来，作为y0的估计。举个例子来说，如果要估计x=0.5时y的取值，先构造一扇窗子(0,1)，那么只有x取值在这个范围内的点才能进入；假定进入窗子的点有(0.2, 1)(0.4, 0.5)(0.8, 0.2)三个，其权重假定为0.2、0.6和0.2，那么x=0.5时y取值的估计就是0.21+0.60.5+0.2*0.2=0.54。在实际计算的时候，窗子的宽度怎么定，窗内点的权重怎么定，是主要要讨论的内容。上面那幅图左边的最近邻法比较简单，就是对离x0最近的k个点取算术平均，而右边的则相对复杂些，如果感兴趣的话可以看看那本书的第193页。

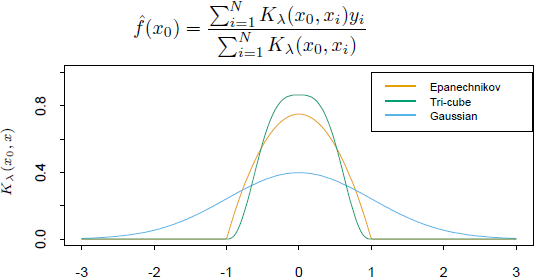
回到正题，在高斯平滑方法中，也基本上是遵循了这条套路，但它的窗子取的是整个实数集，也就是说，图中的所有点都将参与运算，这样一来就只剩下如何确定权重这个问题了。关于这一点，我们应该会有一种直观的感觉，那就是，离我越近的点，我就应该越相信它，因此这个权重很自然地就会取成是两点横坐标之差的函数，而且它应该有两条性质：一是应该关于y轴对称，即在我左边和在我右边是同等待遇；二是离我越远，其权重就应该越小，即满足“亲疏原则”。很显然，正态分布的密度函数就满足这两个条件。以标准正态分布的密度函数φ(x)为例，假设有三个点，离我的距离分别是1，2和3，那么它们权利的大小就分别是φ(1)=0.242，φ(2)=0.054和φ(3)=0.004，相应的权重分别为0.242/(0.242+0.054+0.004)=0.807，0.054/0.3=0.18和0.004/0.3=0.013。我们知道正态分布有两个参数，μ和σ^2，根据前面的对称性原则，μ必须要为0，而σ则可以根据实际情况来变化。一般来说，σ越大，密度曲线就越平坦，等权的倾向也就越大。下面的公式是估计值的表达式，其中的K(,)就是核函数，相当于是不同点“决定权”大小的度量，图中的三条曲线是三种不同的核。

让人感到惊奇的是，这种平滑技术在视觉上的效果就是图像的模糊变化。电脑屏幕上所看到的图像都是由像素点构成的，而颜色则是由一个三维向量(R, G, B)来表示，其中三个分量分别代表了红色、绿色和蓝色的亮度。简单一点，如果只考虑黑白色系，那么颜色就由其“黑的程度”来表达，定义黑为0，白为1，于是任何一种灰色都可以对应到(0, 1)之中的一个实数。想像一下，电脑上的一幅黑白照片其实可以看作是三维空间中的一幅散点图，x轴和y轴分别对应了某个像素点在电脑屏幕上的水平和垂直坐标，z轴则是这个像素点颜色的深浅。要对这幅三维散点图进行平滑，步骤完全一样，只是这时决定权重的函数变成了二元正态分布的密度函数。一般来说，其中的ρ参数都会取成0，即两个分量是相互独立的，而两个方向上的σ则是所谓的X方向和Y方向上的模糊半径。

前面说到，用正态分布来进行平滑，所有的点都要参与运算，这在实际操作中运算量是相当大的。但我们知道，正态密度曲线衰减的速度是比较快的，3σ之后与0相差无几，因此在计算时可以人为地划定一个框（比如3×3或5×5等），只对框内的点进行加权。下面就给出一段R语言程序，用来在R中实现高斯模糊的效果。需要说明的是，这段程序只适用于灰度的jpg或jpeg图片，而且算法没有经过优化，速度可能会非常慢。rimage包和示例图片到这里下载。

#生成“框”中各个元素的权重，grid是框的边长。
gaussm = function(grid, sigma) {
    m = outer(1:grid, 1:grid, function(x, y) dnorm(x - (grid +
        1)/2, 0, sigma) * dnorm(y - (grid + 1)/2, 0, sigma))
    return(m/sum(m))
}
#加载rimage包。
library(rimage)
#指定框的边长和sigma的取值。
grid = 5
sigma = 3
#生成框。
m = gaussm(grid, sigma)
#读取图片，这段程序中需要灰度的jpg或jpeg图片。
pic = read.jpeg("demo.jpg")
#把图片转成像素矩阵。
picm = pic[, ]
newm = picm
r = (grid - 1)/2
#对像素点逐一进行转换，为了简便起见没有包括图片边缘上的点。
for (i in (r + 1):(ncol(picm) - r)) {
    for (j in (r + 1):(nrow(picm) - r)) {
        newm[j, i] = sum(picm[(j - r):(j + r), (i - r):(i + r)] *
            m)
    }
}
#画出原来的图片。
plot(pic)
#新开一个窗口，画出高斯模糊后的图片。
x11()
plot(imagematrix(newm))

更新后的代码，速度应该更快，而且支持彩色图片，可以更换核函数（参数kernelf），感谢Linlin Yan：

blur<-function(x,grid,kernelf,...)
{
    if(grid<3) stop("grid should be great than or equal to 3!");
    if(grid%%2==0) stop("grid should be odd number!");
    v=sapply(1:grid-(grid+1)/2,kernelf,...);
    v<-v/sum(v);
    r<-(grid-1)/2;
    newx<-tmp<-x;
    is.grey<-length(dim(x))<3;
    for(i in (r+1):(nrow(x)-r))
    {
        if(is.grey)
        {
            tmp[i,]<-colSums(x[(i-r):(i+r),]*v);
        }else{
            for(k in 1:3)
            {
                tmp[i,,k]<-colSums(x[(i-r):(i+r),,k]*v);
            }
        }
    }
    for(j in (r+1):(ncol(x)-r))
    {
        if(is.grey)
        {
            newx[,j]<-colSums(t(tmp[,(j-r):(j+r)])*v);
        }else{
            for(k in 1:3)
            {
                newx[,j,k]<-colSums(t(tmp[,(j-r):(j+r),k])*v);
            }
        }
    }
    return(newx);
}
kernel.gauss<-function(x,sigma) dnorm(x,0,sigma);
blur.gauss<-function(x,grid,sigma) blur(x,grid,kernel.gauss,sigma=sigma);

library(rimage);
a=read.jpeg("demo.jpg");
m=blur.gauss(a,5,3);
plot(imagematrix(m));